GESCHICHTE DER MATHEMATIK (D-A,RE;L-WP) R. BÖLLING
2 SWS VL pro Woche, Di 10-12 Uhr, UL 6, 2014A
- Voraussetzungen:
- keine
- Inhalt:
- Behandlung wesentlicher Entwicklungsetappen in der Antike
(babylonische, altägyptische, griechische Mathematik
(Euklids ,,Elemente``)), im Mittelalter (Leonardo von
Pisa, Oresme) und in der Neuzeit (u.a. Cavalieri, Newton,
Leibniz, Cauchy, Weierstraß).
- Literatur:
- Wussing, H.: Mathematik in der Antike, Teubner, 1965
Volkert, K.: Geschichte der Analysis, BI.-Wiss.-Verl,
1987
HÖHERE ALGEBRA (ALGEBRA II) (D-A,RE,S; L-IV)
W. KLEINERT
4 SWS VL pro Woche, Mi 11-13 Uhr, RUD 25, 1.115; Fr 11-13 Uhr,
RUD 25, 2.110
- Voraussetzungen:
- Lineare Algebra und Analytische Geometrie I und II;
Algbra I (wünschenswert, aber nicht unabdingbar)
- Inhalt:
- Höhere Ring- und Idealtheorie (noethersche Ringe und
Moduln, Funktionen- und Operatoralgebren, Arithmetik in
Ringen, Polynom- und Potenzreihenalgebren);
Dimensionstheorie der Ringe und affine algebraische
Geometrie; ebene algebraische Kurven; Ring- und
Körpererweiterungen; höhere Galoissche Theorie;
Differentialalgebra; homologische Methoden in der
Algebra; topologische Methoden in der Algebra; graduierte
Ringe und Moduln. Die Vorlesung liefert wesentliche
Grundlagen für die späteren Spezialisierungsgebiete
Algebra, Algebraische Geometrie und Zahlentheorie bei den
Diplomanden. Auch Lehramtsstudenten (Studienräte) und
Studenten der mathematischen Physik können diese
Veranstaltung für ihre Spezialisierung nutzen.
- Übungen:
- 2 SWS pro Woche
Fr 13-15 Uhr, RUD 25, 2.110; W. Kleinert
- Literatur:
- Kunz, E.: Algebra. Wiesbaden, Vieweg, 1994
Bosch, S.: Algebra. Berlin, Springer, 1996
Lang, S.: Algebra. Reading, Addison-Wesley, 3. Aufl.,
1993
- Geplante Fortsetzung:
- SS 2003, 4 SWS VL, 2 SWS UE, Algebraische Geometrie I
- Sprechstunden:
- Dienstag, 11-13 Uhr, RUD 25, 1.426, Tel. 2093-1435
AUSGEWÄHLTE KAPITEL UND ALGEBRAISCHE
GEOMETRIE (MODULI-PROBLEME) (D-A,RE,S) H. KURKE
4 SWS VL pro Woche, Di 11-13 Uhr, RUD 25, 3.110; Mi 15-17 Uhr,
RUD 25, 3.110
- Voraussetzungen:
- Vorlesung Einführung in die Algebraische Geometrie,
Algebra I, möglichst
Algebra II
- Inhalt:
- Einführende Beispiele, Deformationstheorie (lokale
Modulprobleme), Techniken der projektiven Geometrie
(Quotientenschema, Geometric Invarianttheorie).
- Literatur:
- Mumford-Fogarty: Geometric Invariant Theory. Berlin,
Springer, 1982
Newstead: Introduction to moduli problems. Tata-LN, 1978
Viehweg: Quasiproj. Moduli for polarized manifolds.
Springer, 1995
- Sprechstunden:
- Dienstag, 13-16 Uhr, RUD 25, 1.428, Tel. 2093-1808
ALGEBRAISCHE FLÄCHEN (D-A,RE) R.-P. HOLZAPFEL
2 SWS VL pro Woche, Di 15-17 Uhr, RUD 25, 2.101
- Voraussetzungen:
- Algebra II oder Einführung in die Algebraische Geometrie
oder Algebraische Kurven und Riemannsche Flächen
- Inhalt:
- Monoidale Transformation, minimale Modelle,
Klassifikation, Auflösung von Flächensingularitäten,
Kurven und Divisoren, Schnitttheorie, spezielle Flächen.
- Geplante Fortsetzung:
- SS 2003, 4 SWS VL, Picardsche Modulflächen und
Modulformen; SE Anwendung in der Codierungstheorie
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.427, Tel. 2093-1439
MATHEMATISCHE ASPEKTE
DER STRING THEORIE
I (D-A,RE, fak. Physik) B. ANDREAS
2 SWS VL pro Woche, Fr 09-11 Uhr, RUD 25, 3.008
- Inhalt:
- Quantenfeldtheorien in höheren Dimensionen,
Indextheoreme, Calabi-Jan Mannigfaltigkeiten,
Mirrorsymmetrie, Modulare Invarianz und A-D-E
Klassifikation, ADHM Konstruktion, BPS-Zustände,
D-Branes, String Dualitäten.
- Literatur:
- Green; Schwarz; Witten: String Theory, Bd I, II
Griffith; Harris: Algebraic Geometry
Polchinsky, J.: String Theory, Bd. I, II
- Geplante Fortsetzung:
- SS 2003, Mathematische Aspekte der String Theorie II
ALGEBRAISCHE ZAHLENTHEORIE (D-A,RE;
L-IV; fak. Physik) V. HEIERMANN
4 SWS VL pro Woche, Mo 09-11 Uhr, RUD 25, 3.008; Mi 13-15 Uhr,
RUD 25, 2.009
- Voraussetzungen:
- Grundstudium (insbes. Lineare Algebra und Analytische
Geometrie I und II); Grundkenntnisse in der Theorie der
Körpererweiterungen bzw. Galoistheorie erwünscht,
werden aber zu Anfang eingehend wiederholt.
- Inhalt:
- Ziel der Vorlesung ist eine Einführung in die
algebraische Zahlentheorie. Die zu studierenden Objekte
sind die endlichen algebraischen Erweiterungen des
Körpers
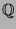 der rationalen
Zahlen. Auf die Analogie mit Funktionenkörpern wird je
nach Verlauf eingegangen. Weitere Stichwörter sind:
Galoistheorie, Dedekindringe, Idealklassengruppe,
Klassenzahl, Dirichletscher Einheitssatz, lokal-global
Prinzip, lokale Körper.
der rationalen
Zahlen. Auf die Analogie mit Funktionenkörpern wird je
nach Verlauf eingegangen. Weitere Stichwörter sind:
Galoistheorie, Dedekindringe, Idealklassengruppe,
Klassenzahl, Dirichletscher Einheitssatz, lokal-global
Prinzip, lokale Körper.
- Übungen:
- 2 SWS pro Woche:
Mo 11-13 Uhr, RUD 25, 3.008; V. Heiermann
- Literatur:
- Koch, H.: Zahlentheorie, algebraische Zahlen und
Funktionen. Vieweg
Neukirch: Algebraische Zahlentheorie. Springer
Fröhlich; Taylor: Algebraic Number Theory
- Geplante Fortsetzung:
- Einführung in die Klassenkörpertheorie und evtl. ihrer
Verallgemeinerungen (Langlandsprogramm)
- Sprechstunden:
- Mittwoch, 11.15 Uhr, RUD 25, 1.112, Tel. 2093-1812
ABELSCHE FUNKTIONEN UND THETAREIHEN (D-A,RE) U. KÜHN
4 SWS VL pro Woche, Mo 13-15 Uhr, RUD 25, 2.009; Do 15-17 Uhr,
RUD 25, 1.115
Voraussetzungen:
Grundkenntnisse in algebraischer Geometrie und/oder komplexer
Analysis.
Inhalt:
Gitter, periodische Funktionen, komplexe Tori, Polarisationen,
abelsche Funktionen,
Thetareihen, Satz von Appel-Humbert
Literatur:
- J. Silverman: Elliptic curves
- C. Birkenhake, H. Lange: Complex abelian varieties
D. Mumford: Abelian varieties
S. Lang: Abelian functions
fällt aus
KOMPLEXE MANNIGFALTIGKEITEN UND HODGETHEORIE (D-A,RE) G. HEIN
HÖHERE ANALYSIS: FUNKTIONALANALYSIS UND
SPREKTRALTHEORIE (D-A,B,RE,AN;L-I,VI,
fak. Physik, Chemie) T. FRIEDRICH
4 SWS VL pro Woche, Di 13-15 Uhr, RUD 25, 1.013; Do 09-11 Uhr,
RUD 25, 1.013
- Inhalt:
- Banach- und Hilbert-Räume, stetige Operatoren.
- Hauptsätze der Funktionalanalysis: Sätze von
Hahn-Banach, von Banach-Steinhaus, vom offenen
Operator und abg. Graphen.
- Integraloperatoren, Integralgleichungen, kompakte
Operatoren.
- Spektrum beschränkter Operatoren, Riesz-Theorie,
Fredholm-Alternative, Hilbert-Schmidt-Theorie,
Satz von Mercer.
- Randwertproblem von Sturm-Liouville.
- Spektraldarstellung selbstadjungierter unitärer
Operatoren.
- Fredholm-Operatoren und deren Index.
- Unbeschränkte Operatoren und deren Spektrum,
Defektindex, Satz von Krein-Krasnosielski, von
Neumann-Sätze, Spektralmaß, Erweiterung
symmetrischer Operatoren.
- Spektralsatz für selbstadjungierte
unbeschränkte Operatoren.
- Übungen:
- 2 SWS pro Woche
UE 1: Di 15-17 Uhr, RUD 25, 2.009; P. Ramacher
UE 2: Do 11-13 Uhr, RUD 25, 2.101; I. Agricola
- Literatur:
- Achieser, N.I.; Glasmann, I.M.: Theorie der linearen
Operatoren im Hilbertraum. Akademie-Verlag Berlin, 1965
Rauch, J.: Partial differential equations. Springer, GTM
128, 1991
Rudin, W.: Functional analysis. McGraw-Hill, 1991
Schwartz, L.: Theorie des distributions. Hermann, 1966
Schwartz, L.: Methodes mathematiques pour les sciences
physiques. Hermann
Vladimirov, V.: Gleichungen der mathematischen Physik.
Dt. Verlag der Wiss., 1972
Zimmer, R.: Essential Results of Functional Analysis.
Chicago University Press, 1990
- Sprechstunden:
- Dienstag, 08-09 Uhr, RUD 25, 1.301, Tel. 2093-1628
fällt aus
FUNKTIONALANALYSIS (D-A,B,RE,AN)
J. NAUMANN Achtung Änderung
Statt der VL Funktionalanalysis
SOBELEV-RÄUME (D-A,
RE, S) J. NAUMANN
2 SWS VL pro Woche, Di 09-11 Uhr, RUD 25, 3.008
-
- Inhalt:
- Schwache Ableitung; Definition und Eigenschaften des
Raumes W m,p; Eigenschaften von Funktionen aus
W m, p; Einbettungssätze.
-
- Literatur:
- wird in der Vorlesung bekannt gegeben
-
MORSE UNGLEICHUNGEN UND
VON NEUMANN INVARIANTEN
(D-A,RE,fak. Physik) G. MARINESCU
2 SWS VL pro Woche, Mo 13-15 Uhr, RUD 25, 3.007
- Voraussetzungen:
- Analysis I - IV
- Inhalt:
- Die Vorlesung hat zum Ziel, die Morsetheorie und einige
Anwendungen in Topologie und Globale Analysis
darzustellen. Die Morsetheorie gestattet, aus der Art und
Anzahl der kritischen Punkte einer Morsefunktion auf
einer Mannigfaltigkeit, Rückschlüsse auf die
topologischen Eigenschaften der Mannigfaltigkeit zu
ziehen. Der differentialtopologische als auch E. Wittens
"Physiker" Beweis werden beschrieben. Dieser
Beweis hatte großen Einfluß, und führte u.a. zur Floer
Homologie. Wir behandeln auch eine von Novikov und Shubin
entwickelte Version für
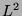 Betti Zahlen (d.h. von Neumann
Dimension der Kohomologiegruppen). Atiyahs
Betti Zahlen (d.h. von Neumann
Dimension der Kohomologiegruppen). Atiyahs  Index
Satz und Gromovs Lösung der Hopfschen Vermutung werden
dargestellt.
Index
Satz und Gromovs Lösung der Hopfschen Vermutung werden
dargestellt.
- Literatur:
- Milnor, J.: Morse theory. Ann. Math. Studies 51,
Princeton, 1963
Witten, E.: Supersymmetry and Morse theory. J. Diff.
Geom., 17 (1982), 661-692
Cycon, H. et al.: Schrödinger Operators with
Applications to Quantum Mechanics and Global Geometry.
Springer, 1987
Shubin, M.: Semiclassical Asymptotics on covering
manifolds and Morse inequalities. GAFA, 6, 1996
- Geplante Fortsetzung:
- SS 2003; Thema noch offen
- Sprechstunden:
- Dienstag, 13-15 Uhr, RUD 25, 1.308, Tel. 2093-1804,
e-mail: george@mathematik.hu-berlin.de, web:
www.mathematik.hu-berlin.de/
 george/VL.html
george/VL.html
ASPEKTE BEI DER MODELLIERUNG UND MATHEMATISCHEN
BEHANDLUNG VON REAKTIONS-DIFFUSIONSPROBLEMEN (D-A,RE) A. GLITZKY
2 SWS VL pro Woche, Fr 11-13 Uhr, RUD 25, 2.101
- Voraussetzungen:
- Analysis I-IV, Funktionalanalysis
- Inhalt:
- Wir betrachten Modelle für die Umverteilung von Teilchen
über die Mechanismen Diffusion und Reaktionen. Ein
wichtiges Beispiel hierfür sind Gleichungssysteme, die
bei der Halbleitertechnologiemodellierung entstehen. Mit
Methoden der konvexen Analysis beweisen wir energetische
Abschätzungen. Wir leiten Grenzmodelle unter Annahmen
über unterschiedliche Zeitskalen für die einzelnen
Teilprozesse her. Diese Reduktion der Modellgleichungen
läßt sich als Galerkin-Schema für das Ausgangsproblem
interpretieren. Wir übertragen Aussagen zu energetischen
Abschätzungen vom Ausgangsproblem auf die reduzierten
Modelle.
- Literatur:
- Gajewski; Gröger; Zacharias: Nichtlineare
Operatorgleichungen und Operatordifferentialgleichungen
Ioffe; Tichomirov: Theory of extremal problems
Ekeland; Temam: Convex Analysis and variational problems
Glitzky, A.: Elektro-Reaktions-Diffusionssysteme mit
nichtglatten Daten
- Geplante Fortsetzung:
- nein
- Sprechstunden:
- nach Vereinbarung, WIAS, Mohrenstr. 39, Tel. 2037-2568,
NICHTGLATTE ELLIPTISCHE RANDWERTPROBLEME
(D-A,RE,AN,S) J. GRIEPENTROG
2 SWS VL pro Woche, Do 09-11 Uhr, RUD 25, 3.011
- Voraussetzungen:
- Analysis I-IV, Lineare Funktionalanalysis, Lebesgue- und
Sobolev-Räume
- Inhalt:
- Lineare elliptische Randwertaufgaben in
Variationsformulierung, Probleme mit nichtglatten Daten,
Existenz und qualitative Eigenschaften von Lösungen der
entsprechenden Variationsgleichungen, Regularität und
Stabilität der Lösungen in Sobolev-Campanato-Räumen.
- Literatur:
- wird noch bekannt gegeben
- Sprechstunden:
- nach Vereinbarung, WIAS, Mohrenstr. 39, Tel. 2037-2551
NICHTLINEARE PARTIELLE DIFFERENTIALGLEICHUNGEN
(D-A,RE,AN;L-I,VI) O. KLEIN
2 SWS VL pro Woche, Mi 09-11 Uhr, RUD 25, 2.101
- Voraussetzungen:
- Analysis I-III, Funktionalanalysis, Lineare partielle
Differentialgleichungen
- Inhalt:
- Existenz und Regularität schwacher Lösungen für
nichtlineare elliptische und parabolische
Differentialgleichungen und Variationsgleichungen
(Monotonie-, Variations-, und Kompaktheitsmethoden);
Systeme von Differentialgleichungen.
- Literatur:
- Barbu, V.: Nonlinear semigroups and differential
equations in Banach spaces. Noordhoff International
Publishing, 1976
Wloka, J.: Partielle Differentialgleichungen. Teubner
Verlag, 1982
Weitere Literatur wird in der Vorlesung bekannt gegeben.
-
- Geplante Fortsetzung:
- SS 2003, 2 SWS SE, Partielle Differentialgleichungen
- Sprechstunden:
- nach Vereinbarung, WIAS, Mohrenstr. 39, Tel. 2037-2533
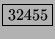
-THEORIE IN KOMPLEXER ANALYSIS UND
ALGEBRAISCHER GEOMETRIE IV (D-A,RE) J. LEITERER
2 SWS VL pro Woche, Mo 15-17 Uhr, RUD 25, 1.114
- Inhalt:
- Dies ist die Fortsetzung entsprechender Vorlesungen in
den vorangegangenen drei Semestern. Gewisse Vorkenntnisse
in Funktionalanalysis und Differentialgeometrie
vorausgesetzt, kann die Vorlesung auch unabhängig davon
gehört werden. Welche Vorkenntnisse das sind, zeigt am
besten ein Blick in das Skript, das parallel zu der
Vorlesungsreihe entsteht und dessen aktuelle Version
jederzeit unter leiterer@mathematik.hu-berlin.de
abgerufen werden kann.
- Literatur:
- Demailly, J.-P.: Complex analytic and algebraic geometry,
http://www-fourier.ujf-grenoble.fr/demailly/books.html
- Geplante Fortsetzung:
- evtl. im SS 2003, 2 SWS VL, gleiches Thema
- Sprechstunden:
- Dienstag, 13-15 Uhr, RUD 25, 1.104, Tel. 2093-1807
DIFFERENTIALGEOMETRIE I (D-A,RE;L-I,III,fak. Physik) H.
BAUM
4 SWS VL pro Woche, Mo 13-15 Uhr, RUD 25, 1.115; Mi 09-11 Uhr,
RUD 25, 3.007
- Voraussetzungen:
- Analysis I, II, Lineare Algebra und Analytische Geometrie
I, II
- Inhalt:
- Topologische Räume und differenzierbare
Mannigfaltigkeiten, Einführung in die Riemannsche
Geometrie (Metriken, Krümmungen, geodätische Linien,
Zusammenhang zwischen Krümmung und Topologie).
- Übungen:
- 2 SWS pro Woche:
Mi 11-13 Uhr, RUD 25, 3.007; T. Neukirchner, T. Leistner
- Literatur:
- wird in der Vorlesung angegeben
- Geplante Fortsetzung:
- SS 2003, Differentialgeometrie II
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.307, Tel. 2093-1823
KLASSISCHE MECHANIK
UND SYMPLEKTISCHE GEOMETRIE (D-A,RE;fak. Physik) K. MOHNKE
4 SWS VL pro Woche, Mo 09-11 Uhr, RUD 25, 3.110; Mi 13-15 Uhr,
RUD 25, 3.110
- Inhalt:
- Diese Vorlesung ist als eigenständige Einführung in die
symplektische Geometrie gedacht. Teilweise werden
Übungen abgehalten, um die notwendigen Begriffe
einzuführen oder zu wiederholen, wie z.B. Mannigfaltigkeiten,
Vektorfelder, Differentialformen. Das Hauptziel ist
es, an Beispielen der klassischen Mechanik
(Himmelsmechanik, harmonischer Oszillator, Kreisel) die
Natürlichkeit dieses Konzeptes zu erläutern. Eine
Punktmasse oder -ladung wird zum Beispiel vollständig
durch den Phasenraum beschrieben. Das ist ein
sechsdimensionaler euklidischer Raum, der mit dem Produkt
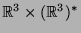 identifiziert
werden kann, der zweite Faktor (der Impuls) ist dabei das
Dual des ersten (der Position). Er besitzt eine
natürliche symplektische Form, d.h. eine
antisymmetrische Bilinearform vom Rang 6:
identifiziert
werden kann, der zweite Faktor (der Impuls) ist dabei das
Dual des ersten (der Position). Er besitzt eine
natürliche symplektische Form, d.h. eine
antisymmetrische Bilinearform vom Rang 6:
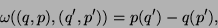
wobei 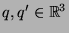 und
und 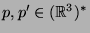 . Die Energie des
Teilchens ist (oft) die Summe aus kinetischer Energie und
dem Potential eines Kraftfeldes:
. Die Energie des
Teilchens ist (oft) die Summe aus kinetischer Energie und
dem Potential eines Kraftfeldes:
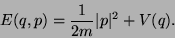
Falls 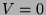 ist, sprechen wir von einem freien Teilchen.
Position und Impuls sind Funktionen der Zeit, die die
Hamilton-Jacobi-Gleichungen erfüllen:
ist, sprechen wir von einem freien Teilchen.
Position und Impuls sind Funktionen der Zeit, die die
Hamilton-Jacobi-Gleichungen erfüllen:
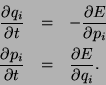
Da die symplektische Form vollen Rang hat, gibt es zu
jedem Punkt  einen eindeutigen
Vektor
einen eindeutigen
Vektor 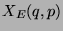 in
in 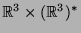 mit
mit
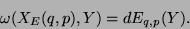
Das definiert ein Vektorfeld auf 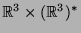 , und die Kurven
des Teilchens im Phasenraum sind dessen Integralkurven.
Energieerhaltung folgt nun einfach aus der Tatsache, daß
, und die Kurven
des Teilchens im Phasenraum sind dessen Integralkurven.
Energieerhaltung folgt nun einfach aus der Tatsache, daß
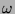 antisymmetrisch ist. Es ist andererseits
nicht schwer einzusehen, daß der Fluß die symplektische
Form erhält. Viele Konzepte der Mechanik
(Erhaltungsgrößen, vollständige Integrabilität) und
der Quantenmechanik (Polarisierung, Heisenberg-Algebra)
lassen sich sehr bequem durch dieses Konzept beschreiben.
antisymmetrisch ist. Es ist andererseits
nicht schwer einzusehen, daß der Fluß die symplektische
Form erhält. Viele Konzepte der Mechanik
(Erhaltungsgrößen, vollständige Integrabilität) und
der Quantenmechanik (Polarisierung, Heisenberg-Algebra)
lassen sich sehr bequem durch dieses Konzept beschreiben.
- Literatur:
- Arnold, V.I.: Mathematische Methoden der klassischen
Mechanik. Springer Verlag
Mehr Literaturangaben in der Vorlesung.
NUMERIK GEWÖHNLICHER
DIFFERENTIALGLEICHUNGEN
(D-B,AN,S;fak.Physik,Informatik) R. MÄRZ
4 SWS VL pro Woche, Mo 11-13 Uhr, RUD 25, 3.110; Mi 09-11 Uhr,
RUD 25, 3.110
- Inhalt:
- Modellierung mit gewöhnlichen Differentialgleichungen;
Standardverfahren zur numerischen Integration (IRK);
asymptotische Lösungseigenschaften und qualitativ
korrekte Reflexion; Korrektheit und Kondition bei
Randwertaufgaben; Diskretisierung; Mehrzielmethoden;
dynamische Iteration.
- Übungen:
- 2 SWS pro Woche:
Mo 13-15 Uhr, RUD 25, 2.101; A. Backes
- Sprechstunden:
- Mittwoch, 13-15 Uhr, RUD 25, 2.415, Tel. 2093-2353
NUMERIK PARTIELLER
DIFFERENTIALGLEICHUNGEN
(D-B,AN,S) C. TISCHENDORF
4 SWS VL pro Woche, Di 09-11 Uhr, RUD 25, 4.008; Fr 11-13 Uhr,
RUD 25, 3.007
- Voraussetzungen:
- Numerik gewöhnlicher Differentialgleichungen
- Inhalt:
- Elliptische Randwertaufgaben, Differenzenverfahren,
Variationsgleichungen und konforme Approximation,
Galerkin-Verfahren, Methode der finiten Elemente,
nichtkonforme Methoden, numerische Behandlung
parabolischer Probleme, Crank-Nicolson-Verfahren,
Linienmethode.
- Übungen:
- 2 SWS pro Woche:
Di 11-13 Uhr, RUD 25, 4.008; R. Lamour
- Literatur:
- Großmann, Ch.; Ross, H.-G.: Numerik partieller
Differentialgleichungen
Ciarlet, P.G.: The finite element method for elliptic
problems
- Sprechstunden:
- Mittwoch, 13-15 Uhr, RUD 25, 2.411, Tel. 2093-2630
ALGEBRO-DIFFERENTIALGLEICHUNGEN B(D-B,AN,S) R. MÄRZ
2 SWS VL pro Woche, Do 09-11 Uhr, RUD 25, 2.110
- Voraussetzungen:
- Vordiplom (Mathematik), Numerische Mathematik, Numerik
gewöhnlicher Differentialgleichungen
- Inhalt:
- Entwicklung und Analyse numerischer Verfahren für
Algebro-Differentialgleichungen (ADGln), Diskussion
verschiedener Lösungskonzepte, Anwendungen, Kriterien
zur Index-Bestimmung.
- Geplante Fortsetzung:
- SS 2003, 2 SWS VL, Algebro-Differentialgleichungen A
- Sprechstunden:
- Mittwoch, 13-15 Uhr, RUD 25, 2.415, Tel. 2093-2353
OPTIMIERUNG I (D-B,AN) B. KUMMER
2 SWS VL pro Woche, Di 09.30-11 Uhr, RUD 25, 2.110
- Inhalt:
- Konvexe Optimierung (Dualität, Subdifferential und
Folgerungen für lineare Probleme),
Optimalitätsbedingungen im nichtkonvexen Fall
(KKT-Bedingungen, Bedingungen 2. Ordnung), Grundlegende
Lösungsmethoden (Simplexmethoden, zulässige Richtungen,
Strafmethoden, Verfahren 2. Ordnung).
- Übungen:
- 1 SWS pro Woche:
Di 11-13 Uhr (1. Woche), RUD 25, 2.110; B. Kummer
- Geplante Fortsetzung:
- SS 2003, Ausgewählte Kapitel der Optimierung, 2 SWS VL
und 1 SWS UE
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.408, Tel. 2093-5844
STOCHASTISCHE OPTIMIERUNG (D-B,AN,S) W. RÖMISCH
2 SWS VL pro Woche, Do 13-15 Uhr, RUD 25, 1.115
- Voraussetzungen:
- Grundkurs Stochastik I und (möglichst) Optimierung I
- Inhalt:
- Zwei- und mehrstufige stochastische Optimierungsmodelle,
Theorie, Stabilität und Lösungsverfahren, Anwendungen
in der Finanz- und Energiewirtschaft.
- Literatur:
- Birge, J.R.; Louveaux, F.: Introduction to Stochastic
Programming. Springer, 1997
Prekopa, A.: Stochastic Programming. Kluwer, 1995
- Sprechstunden:
- Mittwoch, 13-15 Uhr, RUD 25, 2.414, Tel. 2093-2561
fällt aus
REGRESSIONS- UND VARIANZANALYSE (D-B,AN) N.N.
NICHTPARAMETRISCHE VERFAHREN
UND IHRE ANWENDUNGEN (D-B,AN,S;L-V) V. SPOKOINY
2 SWS VL pro Woche, Di 09-11 Uhr, RUD 25, 2.009
- Voraussetzungen:
- Grundausbildung in Stochastik
- Inhalt:
- Grundideen und Eigenschaften moderner statistischer
Schätzverfahren. Anwendungen auf Signal- und
Bildentrauschen, Zeitreihenanalyse, Finanz- und
Biomedizin.
- Sprechstunden:
- Montag, 15-17 Uhr, WIAS, Mohrenstr. 39, Tel. 2037-2575
COMPUTERINTENSIVE STATISTIK (D-B,AN) J. POLZEHL
2 SWS VL pro Woche, Mo 15-17 Uhr, RUD 25, 4.008
STOCHASTIK II (STOCHASTISCHE PROZESSE) (D-B,AN;L-V) H. FÖLLMER
4 SWS VL pro Woche, Di 08-09.30 Uhr, RUD 25, 3.110; Mi 09-11
Uhr, RUD 25, 1.013
- Inhalt:
- Konstruktion stochastischer Prozesse. Martingale in
diskreter Zeit. Brownsche Bewegung.
- Übungen:
- 2 SWS pro Woche:
Mi 13-15 Uhr, RUD 25, 3.007; J. Penner
- Literatur:
- Bauer, H.: Probability Theory. de Gruyter, Studies in
Mathematics, 1996
Durrett, R.: Probability Theory and Examples, Duxbury
Press, 1991
- Geplante Fortsetzung:
- SS 2003, Stochastische Analysis
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.204, Tel. 2093-5817
EINFÜHRUNG IN DIE
STOCHASTISCHE FINANZMATHEMATIK (D-B,AN) P. BANK
3 SWS VL pro Woche, Mo 11-13 Uhr, RUD 25, 3.007; Fr 11-13 Uhr
(1. Woche), RUD 25, 3.110
- Voraussetzungen:
- Stochastik I; es empfielt sich der Besuch der parallel
angebotenen Vorlesung Stochstik II
- Inhalt:
- Die Vorlesung führt in die Theorie zeitdiskreter
Finanzmarktmodelle ein. Im Mittelpunkt steht zunächst
die Charakterisierung arbitragefreier Modelle durch die
Existenz von Martingalmaßen mit Hilfe
funktionalanalytischer Trennungssätze.
Martingaltheoretische Methoden ermöglichen dann die
konsistente Bewertung von Finanzderivaten wie z.B.
Call-Optionen und die Beschreibung von
Absicherungsstrategien gegen die mit solchen Derivaten
verbundenen Risiken. Es zeigt sich dabei, daß in
zeitdiskreten Modellen eine perfekte Absicherung in der
Regel unmöglich ist. Die Bestimmung effizienter
Absicherungsstrategien, die Risiko und Kapitaleinsatz
bestmöglich abwägen, führt auf stochastische
Optimierungsprobleme, die mit Mitteln der konvexen
Analysis gelöst werden.
- Übungen:
- 1 SWS pro Woche:
Fr 11-13 Uhr (2. Woche), RUD 25, 3.110
- Sprechstunden:
- nach Vereinbarung, ZI 13a, 603, Tel.: 2093-1450
STOCHASTISCHE DIFFERENTIALGLEICHUNGEN
MIT GEDÄCHTNIS (D-A,B,RE,AN,S;L-I,V) M.
REISS
2 SWS VL pro Woche, Do 09-11 Uhr, RUD 25, 4.008
- Voraussetzungen:
- Grundstudium Analysis und Stochastik; auf fehlende
Vorkenntnisse in stochastischen Prozessen oder höherer
Analysis wird nach Bedarf eingegangen.
- Inhalt:
- Zeitverzögerte Phänomene, die zufälligen Störungen
unterliegen, treten in vielen Anwendungen auf. Ihre
mathematische Behandlung führt auf eine reizvolle
Verbindung von analytischen und stochastischen Methoden.
Stichpunkte: math. Grundlagen; Existenz, Eindeutigkeit
und Eigenschaften von Lösungen; Lyapunov-Funktionale;
lineare Gleichungen; Beispiele aus Biologie, Physik,
Ökonomie. Je nach Hörerwunsch: Behandlung als
stochastische Evolutionsgleichungen im Hilbertraum oder
Anwendungen in Statistik und Optimierung.
- Literatur:
- Hale, J.; Verdayn Lanel, S.: Introduction to Functional
Differential Equations. Springer-Verlag, 1993
Mao, X.: Stochastic Differential Equations and their
Applications. Horwood Publishing, 1997
- Geplante Fortsetzung:
- Im Anschluss ist ein vertiefendes Seminar möglich
- Sprechstunden:
- Dienstag, 10-11 Uhr, RUD 25, 1.210, Tel. 2093-5874
EINFÜHRUNG IN DIE
MATHEMATISCHE LOGIK
(D-C,RE;L-VII) A. BAUDISCH
4 SWS VL pro Woche, Mo 11-13 Uhr, RUD 25, 1.013; Mi 09-11 Uhr,
RUD 25, 1.115
- Inhalt:
- In der VL werden die grundlegenden Begriffe der
mathematischen Logik eingeführt, wobei der
Prädikatenkalkül erster Stufe im Mittelpunkt steht.
Höhepunkte der VL sind die Gödelschen Sätze.
- Übungen:
- 2 SWS pro Woche:
Mo 13-15 Uhr, RUD 25, 4.007; A. Baudisch
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.403, Tel. 2093-5824
ELEMENTE DER ALGEBRA
UND AUFBAU DER ZAHLBEREICHE
(L-IV) J. KRAMER
4 SWS VL pro Woche, Di 11-13 Uhr, RUD 25, 1.115; Fr 09-11 Uhr,
RUD 25, 1.115
- Inhalt:
- 1. Elemente der Gruppentheorie (Halbgruppe,
Gruppe, Untergruppe, Normalteiler, Homomorphismus,
Homomorphiesatz, Beispiele). Einbettung einer
kommutativen, regulären Halbgruppe in eine minimale,
kommutative Gruppe; Anwendung: Konstruktion von
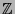 aus
aus 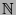 .
.
2. Elemente der Ringtheorie (Ring, Unterring,
Ideal, Homomorphismus, Homomorphiesatz, Beispiele).
Integritätsbereiche, faktorielle Ringe, Hauptidealringe,
Euklidische Ringe, Schiefkörper, Körper. Einbettung
eines Integritätsbereiches in einen minimalen Körper
(Quotientenkörper); Anwendung: Konstruktion von 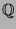 aus
aus 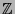 .
.
3. Abschluß des Aufbaus der Zahlbereiche:
Konstruktion von 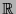 aus
aus 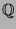 (Cauchyfolgen / Dedekindsche Schnitte / Axiomatischer
Zugang). Konstruktion der Hamilton'schen Quaternionen.
(Cauchyfolgen / Dedekindsche Schnitte / Axiomatischer
Zugang). Konstruktion der Hamilton'schen Quaternionen.
4. Elementare Arithmetik von 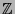 : Unendlichkeit
der Primzahlmenge, Fundamentalsatz der Zahlentheorie
(d.h.
: Unendlichkeit
der Primzahlmenge, Fundamentalsatz der Zahlentheorie
(d.h. 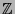 ist faktoriell).
ist faktoriell). 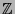 als
Euklidischer Ring,
als
Euklidischer Ring, 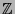 als
Hauptidealring. Bestimmung des größten gemeinsamen
Teilers über Primfaktorzerlegung bzw. mit Hilfe des
Euklidschen Algorithmus.
als
Hauptidealring. Bestimmung des größten gemeinsamen
Teilers über Primfaktorzerlegung bzw. mit Hilfe des
Euklidschen Algorithmus.
5. Elementare Kongruenzlehre: Der Restklassenring 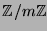 , die
multiplikative Gruppe von
, die
multiplikative Gruppe von 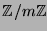 , die Eulersche
, die Eulersche 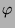 -Funktion.
Der kleine Fermat'sche Satz, Elemente der Kryptographie
(RSA-Verschlüsselung). Lösen simultaner Kongruenzen.
Quadratische Reste einschließlich des Gauß'schen
Reziprozitätsgesetzes.
-Funktion.
Der kleine Fermat'sche Satz, Elemente der Kryptographie
(RSA-Verschlüsselung). Lösen simultaner Kongruenzen.
Quadratische Reste einschließlich des Gauß'schen
Reziprozitätsgesetzes.
- Übungen:
- 2 SWS pro Woche:
Di 13-15 Uhr, RUD 25, 2.110; A. Filler
- Sprechstunden:
- Mo, 11-12 Uhr, UL 6, 3048, Tel. 2093-5815
AUSGEWÄHLTE KAPITEL
DER ELEMENTARGEOMTRIE I. LEHMANN
2 SWS VL pro Woche, März 2003
- Inhalt:
- Es werden zentrale Begriffe und Sätze der
Elementargeometrie behandelt, ihre Bedeutung und
gegenseitige Abhängigkeiten werden untersucht. Typische
Übungsaufgaben werden gehört. (Nutzbar zur Vorbereitung
auf die Staatsprüfung)
AUSGEWÄHLTE KAPITEL
DER WAHRSCHEINLICHKEITSRECHNUNG E. WARMUTH
2 SWS VL pro Woche, März 2003
- Inhalt:
- Es werden zentrale Begriffe und Sätze wiederholt, ihre
Bedeutung und gegenseitige Abhängigkeit untersucht und
typische Aufgaben gelöst (nutzbar zur Vorbereitung auf
die Staatsprüfung).
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.309, Tel. 2093-5830
Zusätzliche Lehrveranstaltung
Einführung in die Theorie
probabilistischer Interaktionssysteme mit Anwendungen in der
Ökonomie
U. Horst
2 SWS VL pro Woche, Di 13-15 Uhr, RUD 25,
3.110
Voraussetzungen: Stochastik
I; möglichst auch Stochastik II
Inhalt: Die
Vorlesung führt in die Theorie interagierender Teilchensysteme
ein und behandelt Anwendungsbeispiele derartiger Systeme in den
Wirtschaftswissenschaften. Hierzu werden zunächst die
mathematischen Grundlagen (Markovsche Prozesse in stetiger Zeit,
Erzeuger, Halbgruppen, Hille-Yosida Theorem, ...) vermittelt.
Anschließend wird das stochastische Ising Modell sowie ggf. das
Voter Modell besprochen. Hierbei soll besonders der Zusammenhang
zwischen der Ergodizität des Ising Modells und dem Auftreten von
Phasenübergängen bei Gibbs Maßen aufgezeigt werden. Es folgen
dann Anwendungsbeispiele aus den Bereichen Mikroökonomie,
Spieltheorie und ggf. Kreditrisiken.
Literatur: Liggett,
T., (1985) Interacting Particle Systems, Springer, Grundlehren
der mathematischen Wissenschaften 276.
Blume,
L. (1993) The Statistical Mechanics of Strategic Interaction,
Games and Economic Behavior, 5, 387-427.
Föllmer,
H. (1974) Random Economies with Many Interacting Agents, J. Math.
Econ., 1, 51-62.
Rene Lamour 2002-10-30
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() und
und ![]() . Die Energie des
Teilchens ist (oft) die Summe aus kinetischer Energie und
dem Potential eines Kraftfeldes:
. Die Energie des
Teilchens ist (oft) die Summe aus kinetischer Energie und
dem Potential eines Kraftfeldes: ![]()
![]() ist, sprechen wir von einem freien Teilchen.
Position und Impuls sind Funktionen der Zeit, die die
Hamilton-Jacobi-Gleichungen erfüllen:
ist, sprechen wir von einem freien Teilchen.
Position und Impuls sind Funktionen der Zeit, die die
Hamilton-Jacobi-Gleichungen erfüllen: 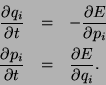
![]() einen eindeutigen
Vektor
einen eindeutigen
Vektor ![]() in
in ![]() mit
mit ![]()
![]() , und die Kurven
des Teilchens im Phasenraum sind dessen Integralkurven.
Energieerhaltung folgt nun einfach aus der Tatsache, daß
, und die Kurven
des Teilchens im Phasenraum sind dessen Integralkurven.
Energieerhaltung folgt nun einfach aus der Tatsache, daß
![]() antisymmetrisch ist. Es ist andererseits
nicht schwer einzusehen, daß der Fluß die symplektische
Form erhält. Viele Konzepte der Mechanik
(Erhaltungsgrößen, vollständige Integrabilität) und
der Quantenmechanik (Polarisierung, Heisenberg-Algebra)
lassen sich sehr bequem durch dieses Konzept beschreiben.
antisymmetrisch ist. Es ist andererseits
nicht schwer einzusehen, daß der Fluß die symplektische
Form erhält. Viele Konzepte der Mechanik
(Erhaltungsgrößen, vollständige Integrabilität) und
der Quantenmechanik (Polarisierung, Heisenberg-Algebra)
lassen sich sehr bequem durch dieses Konzept beschreiben.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()