ECMath SE5: Optimal design and control of optofluidic solar steerers and concentrators
|



|
|||||||||
Background and aim of the project
|
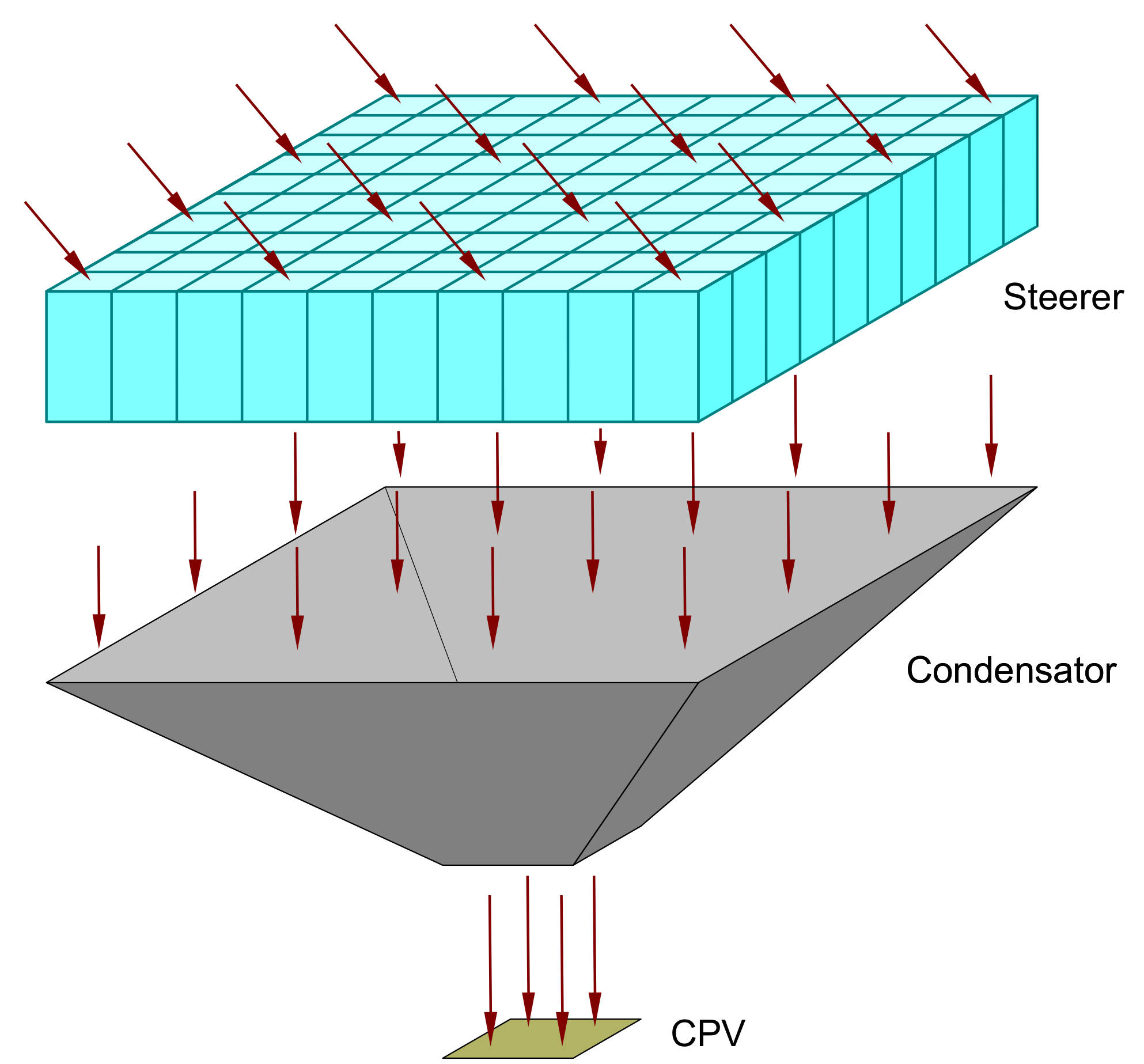
Solar energy is mostly harvested by means of photovoltaic (PV) or concentrating photovoltaic (CPV) solar cells.
The efficiency of CPV is higher (at least twice) than the traditional PV but significantly more expensive.
To reduce costs, optical condensers (e.g., a Fresnel lens) to concentrate solar light on each CPV cell are used.
Moreover, since the energy production is maximized when the panels are perpendicular to the light beam,
mechanical tracking systems that move the array of solar panels based on the position of the sun.
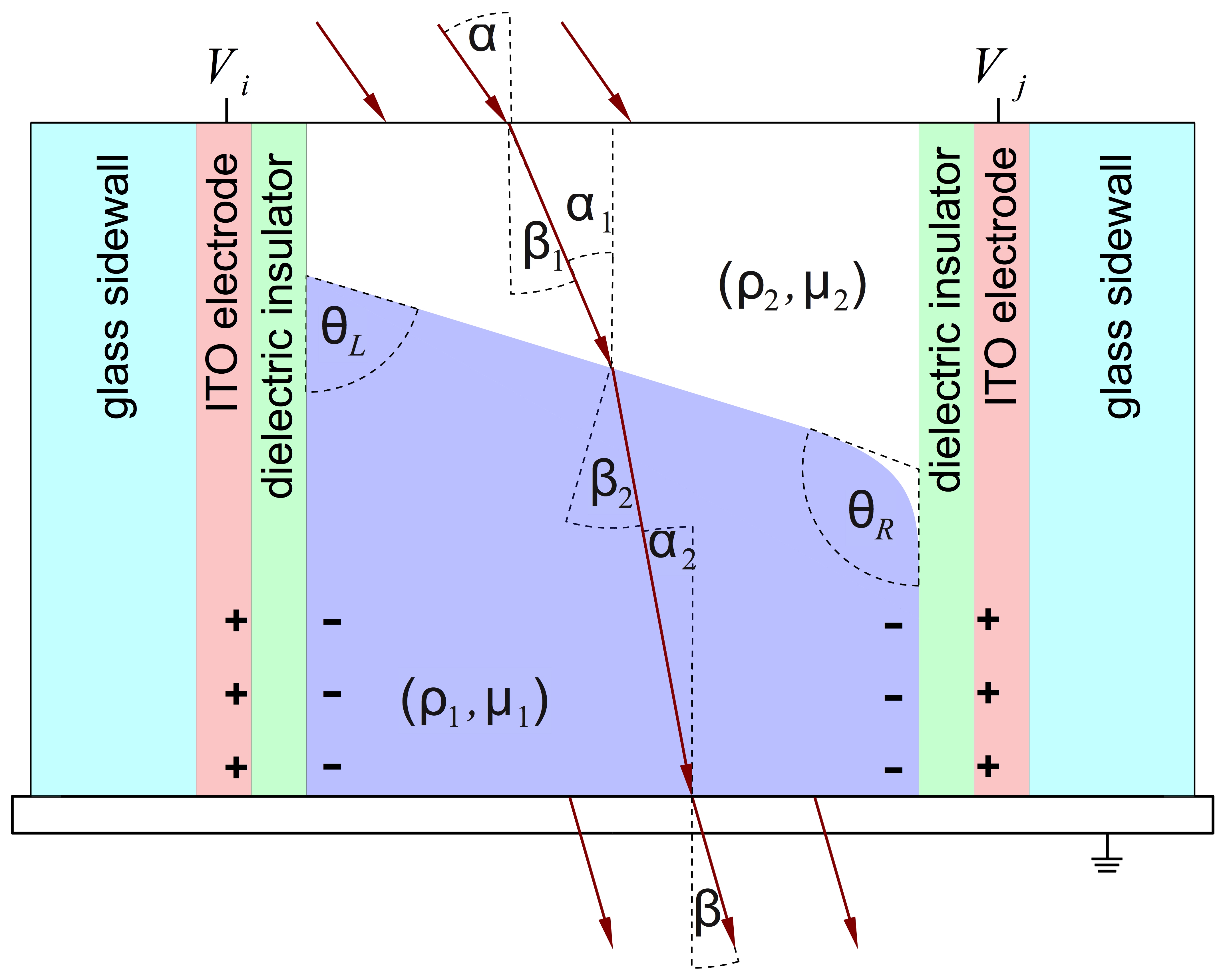
But these tracking system increases costs, requires power and are error-prone. The goal of this project is the optimal design and control of steerers and concentrators for PV or CPV using electrowetting (EW) and electrowetting-on-dielectric (EWOD). The EWOD effect allows to control the shape and contact angle of a droplet-shaped electrolyte with a dielectric surface by the application of electric signals. With either two immiscible liquids, or a liquid and a gas, this control of the shape of the interface changes the deflections of incoming light and can be used to steer a beams in a desired direction and/or to concentrate it. |
|
|
The underlying optimization task is as follows: Assume that Γd is the desired shape of the interface between both fluids in either the liquid-liquid or gas-liquid configurations. Such a shape is provided externally based on a known or sensed trajectory of the light source. The main objective amounts to solving a minimization problem for the unknown voltage actuator (V) to be applied and that is located in the wall of the container so that the real interface Γ comes as close as possible to the desired interface Γd while accounting for the costs of the control action. Apart from the equations of motion of the fluids this optimization task may be additionally subject to further constraints. |
Mathematical details
Liquid-liquid configuration
In the case of two liquids, we use a phase-field model where the macroscopically immiscible fluids are allowed to mix in a small interface region. The evolution is modeled by the Cahn-Hilliard/Navier-Stokes system with variable densities by Abels, Garcke, Grün.
| Here, the relative concentration φ acts as an order parameter and takes the values +1 or -1 for the pure phases, respectively. The mean fluid velocity is given by u, ρ is the fluid density which is supposed to be affine function depending on φ with derivative given by ϑ, ν is the viscosity coefficient, p the pressure, μ the chemical potential, m the mobility, Ψ the double-obstacle potential and F the effect of the control V on the system. |
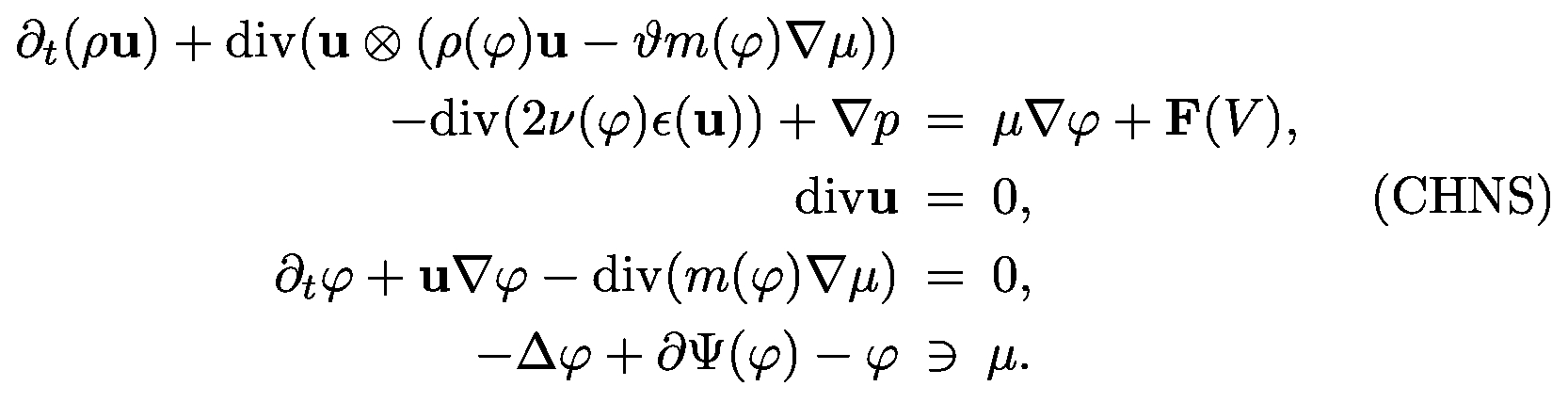
|
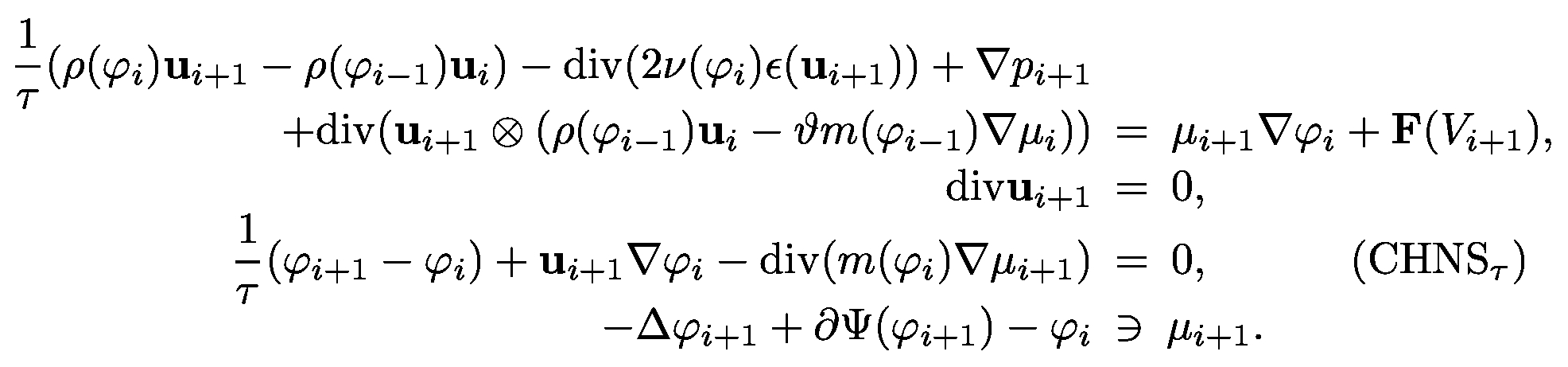
|
For its numerical realization, we consider a suitable time-discretization of (CHNS) that allows the derivation of energy estimates. This estimates are crucial for the analytical treatment of the corresponding optimization problem. |
The optimization task consists in finding a control V and a corresponding solution (φ,μ,u) to a given number of consecutive points in time and minimizing the desired cost functional J (typically of tracking type):
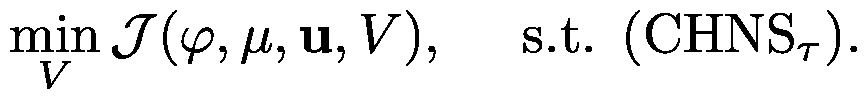
Gas-liquid configuration
In the case that one of the fluids is a gas we use a models given by Walker. Here, the problem is reduced to the following Hele-Shaw type system in two dimensions with an additional inertial term and contact line pinning and a moving interface which is driven by curvature.
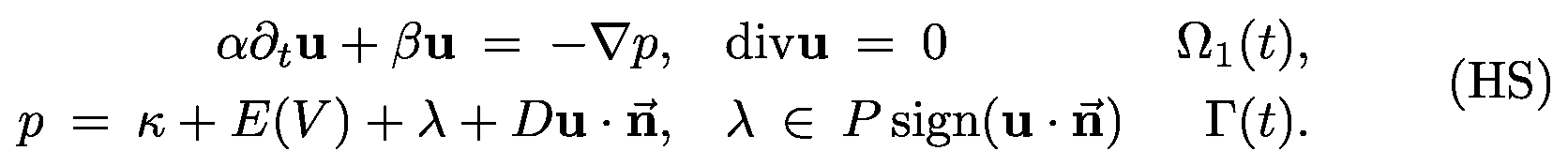
|
The curvature of the interface Γ(t) is denoted by κ, D and P are coefficients of viscous damping and α and β are positive real numbers. |
| For system (HS) we consider a suitable time-discretization. Here, the curvature κ is replaced by an approximation corresponding to the new interface. |
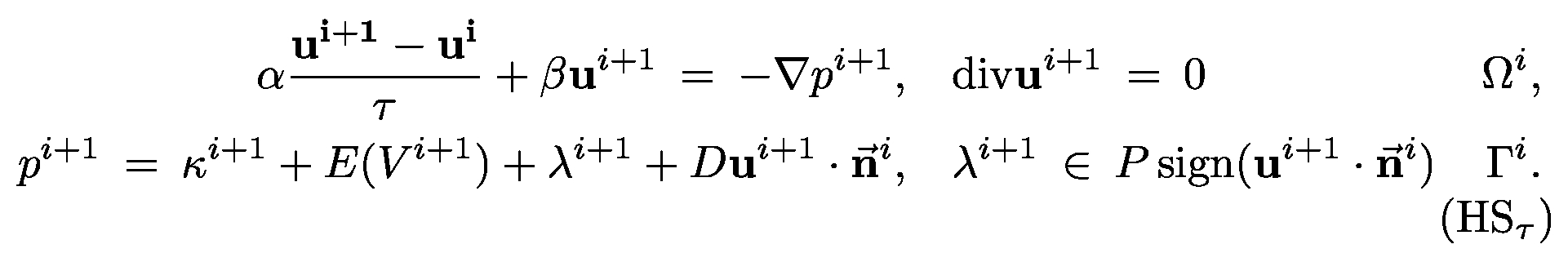
|
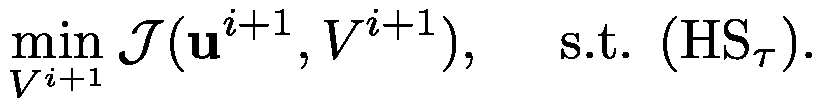
Challenges and results
Both optimization problems are non-convex and non-smooth with state systems involving variational inequalities rendering the problems Mathematical Programming with Equilibrium Constraints (MPECs). In the liquid-liquid as well as in the liquid-gas configuration we proved the existence of minimizers and derived first order optimality systems for a family of smooth approximations of the optimization problem. This is done by regularizing the variational inequalities by a Yosida type approximation. Moreover, stationary points for the original problem were derived via limit processes. The resulting stationary stationarity system for the original problem is established which is related to a function space version of C-stationarity. In order to tackle the problem numerically, we developed a solution technique for the liquid-liquid configuration based on a goal-oriented dual-weighted adaptive finite elements method, which is currently being implemented.
Publications
| [1] | H. Antil, M. Hintermueller, R.H. Nochetto, T.M. Surowiec and D. Wegner. Finite Horizon Model Predictive Control of Electrowetting on Dielectric with Pinning. Submitted to Interfaces and Free Boundaries, 2015. | |
| [2] | S. Hajian, M. Hintermüller, S. Ulbrich. Total variation diminishing schemes in optimal control of scalar conservation laws. IMA Journal of Numerical Analysis, DOI: 10.1093/imanum/drx073, 2017. | |
| [3] | M. Hintermüller, R. H. W. Hoppe, and C. Löbhard. Dual-weighted goal-oriented adaptive finite elements for optimal control of elliptic variational inequalities. ESAIM Control Optim. Calc. Var., 20(2):524-546, 2014. | |
| [4] | M. Hintermüller, M. Hinze, C. Kahle, T. Keil. A goal-oriented dual-weighted adaptive finite elements approach for the optimal control of a Cahn-Hilliard-Navier-Stokes system. WIAS Preprint 2311, 2016. | |
| [5] | M. Hintermüller, T. Keil, D. Wegner. Optimal Control of a Semidiscrete Cahn-Hilliard-Navier-Stokes System with Non-Matched Fluid Densities. SIAM J. Control Optim., 55(3):1954-1989, 2017. | |
| [6] | M. Hintermüller, T. Surowiec. A PDE-constrained generalized Nash equilibrium problem with pointwise control and state constraints. Pac. J. Optim., 9(2):251-273, 2013. | |
| [7] | M. Hintermüller, D. Wegner. Distributed and boundary control problems for the semidiscrete Cahn-Hilliard/Navier-Stokes system with nonsmooth Ginzburg-Landau energies. Topological optimization and optimal transport, Radon Ser. Comput. Appl. Math., 17:40-63, 2014. |
References
| [1] | H. Abels, H. Garcke, G. Grün. Thermodynamically consistent, frame indifferent diffuse interface models for incompressible two-phase flows with different densities. Math. Models Methods Appl. Sci., 22, 2012. | |
| [2] | S. W. Walker, A. Bonito, R. H. Nochetto, Mixed finite element method for electrowetting on dielectric with contact line pinning. Interfaces Free Bound., 12:85-119, 2010. |